Gradient Descent
이는 현실적으로 Loss Function의 최소값을 구하기 위해 고안된 방법으로 아래의 식으로 구한다.
$$W^{(n+1)}=W^{(n)}-\gamma_W \frac{\delta_{Loss}}{\delta_{W}}$$
$$b^{(n+1)}=b^{(n)}-\gamma_b \frac{\delta_{Loss}}{\delta_{b}}$$
여기서 $\gamma_W$는 learning rate로 각 epoch마다 기울기를 얼마나 변화시킬지, 즉 밑에 나오는 그래프에서 얼마나 이동할지 거리를 결정하는 매개변수이다.
그리고 $-\frac{\delta_{Loss}}{\delta_{b}}$는 기울기와 반대방향으로 진행한다는 의미이다. 이게 무슨소리인가하면

위의 그림을 살펴보면 최소값으로 향하기 위해서는 기울기의 반대방향으로 진행해야한다.
- 기울기가 음인 경우에는 양의 방향으로 가야 극소점으로 이동한다.
- 기울기가 양인 경우에는 음의 방향으로 가야 극소점으로 이동한다.
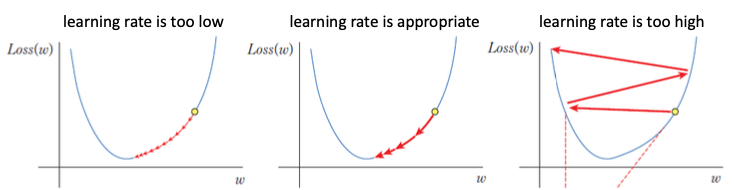
Learning rate
Learning rate에 대해 조금더 알아보면 lr이 너무 작으면 학습 속도가 느리고 너무 크면 최소점을 지나버린다.
따라서, 적절한 lr을 선택하는 것이 모델 훈련에 중요한 요소이다.
Local Minima

머신러닝 분야의 고질적인 문제인데 Loss Function을 평면이나 공간에 표현했을때 여러개의 극소점이 존재하게 되는데
그 중에서 전역적으로 최소인 점은 1개이다. 하지만 모델이 학습과정에서 위의 파란 선과같은 과정을 통해 지역국소점에 빠지게 되면
이를 빠져나올 방법이 사실 없다. 왜냐하면 복잡한 모델의 경우 위 그림처럼 나타내는것 자체가 불가능하기 때문이다.
아래는 GD 식이다.

GD 병렬 계산
GD를 계산할때 W, b를 아래와 같이 병렬적으로 계산할 수 있다.
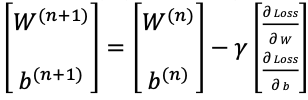
Loss(W,b)에 대해서 기울기 값 Gradient는 아래와 같이 표현한다.

높은 차원의 Loss(W,b)에 대해서도 GD로 동일하게 계산한다.
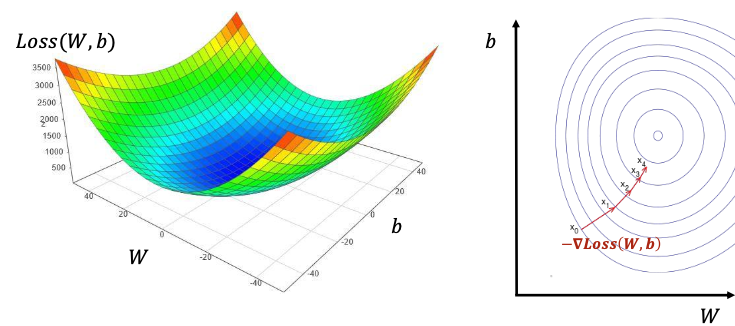
오른쪽은 W,b에 대해서 그린 등고선이다. 최솟값은 가운데 점이므로 기울기의 반대 방향을 따라서 가운데 점으로 이동한다.
가중치가 여러 개인 일반적인 경우 $f(x)=Wx$ 식이 있을때 가중치 W와 x는 아래와 같은 행렬이다.
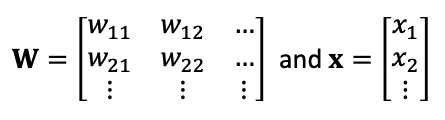
그리고 Gradient Descent 값은 $$ W^{(n+1)}=W^{(n)}-\gamma \Delta_{W} Loss(W^{(n)}) $$
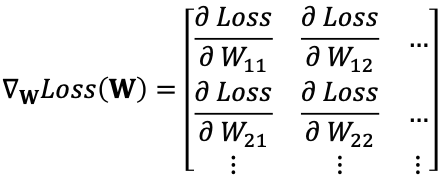
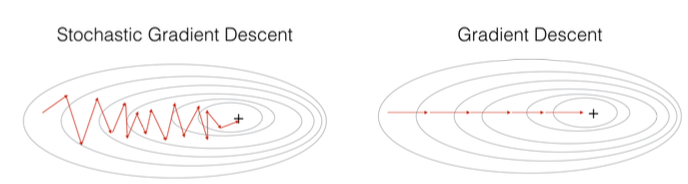
Stochastic Gradient Descent
기존의 GD는 Loss Function의 값을 구할때 모든 데이터에 대해서 Loss값을 구한후 다 더해서 데이터의 총 수로 나눠줬다.

하지만 이러한 방식은 계산량이 많고 오래 걸린다.
전체 데이터셋에 대해서 Gradient를 평가하는 기존 방식에서 벗어나서 SGD는 데이터를 여러 개의 부분집합(mini-batch)으로 나누고 gradient를 계산하고 가중치를 업데이트한다.

SGD는 GD에 비해 연산량이 적고 빠르지만 더 "oscillate" 또는 "진동"한다. 진동한다는 의미는 목적지를 향해 갈때 좌우로 더 움직이는 것을 뜻한다.
'인공지능 > 인공지능 기초 개념' 카테고리의 다른 글
| 기초 개념편 (3) - KNN 모델 (0) | 2024.04.14 |
|---|---|
| 벡터의 크기와 거리(Norm and Distance) (0) | 2024.04.14 |
| 기초 개념편 (2) Linear Regression (0) | 2024.04.14 |
| 기초 개념편 (1) Machine Learning이란? (0) | 2024.04.13 |
| Tensor에 대해 (0) | 2024.03.19 |